Une distribution statistique est symétrique si les observations repérées par leurs fréquences sont également dispersées de part et d'autre d'une valeur centrale. Le coefficient d'asymétrie correspond au moment d'ordre 3* de la variable centrée réduite. En pratique, un utilise un estimateur normalisé et non biaisé égal à :
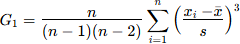
|
Avec : - n le nombre d'observations - xi le score observé pour l'observation i - x̄ et s la moyenne et écart-type non biaisés (**) |
La valeur de ce coefficient d'asymétrie (skewness) est de 0 pour une distribution normale. Un coefficient négatif traduit une asymétrie avec une queue de de distribution plus étendue à gauche. Un coefficient positif traduit une asymétrie avec une queue de de distribution plus étendue à droite.
En général, pour les scores observés dans une épreuve cognitive, un coefficient d'asymétrie positif est en relation avec un effet plancher (tâche difficile) et un coefficient d'asymétrie négatif est en relation avec un effet plafond (tache trop facile).
|
|
|
|
skewness positif |
skewness négatif |
Figure H.1 : Exemples de courbes asymétriques
(*) Pour ceux qui veulent savoir : Un moment d'ordre r est une moyenne des écarts par rapport à un réel "a" élevés à une puissance "r", r étant un entier naturel. La moyenne et la variance sont des moments d'ordre 1 et 2. Le skewness et le kurtosis des moments d'ordre 3 et 4 (facile à comprendre si on inspecte les formules de calcul de ces indices).
(**) Un estimateur non biaisé pour la moyenne et l'écart-type s'obtient en remplaçant n par n-1 dans les formules de la moyenne et de l'écart-type