Corrélation de Spearman

Le rho de Spearman (ρ) est le coefficient de corrélation que l'on utilise lorsque les variables ne sont pas des variables d'intervalle mais des variables ordinales. C'est un test non paramétrique (pas d'hypothèse sur les paramètres). En fait, le principe de ce coefficient est d'appliquer la formule du coefficient de Bravais-Pearson non pas sur les valeurs observées mais sur les rangs (pour chaque variable on remplace le score observé par son rang). Compte tenu de certains propriétés des rangs (par exemple la moyenne de n scores exprimés en rang est égal à (n+1)/2), on donne souvent comme formule de calcul du rho de Spearman une version simplifiée :

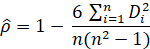
avec :  Di l'écart entre les rangs (pour chaque paire d'observation)

Remarques :

■Lorsqu'il y a des ex-æquos  on affecte comme rang, la moyenne des rangs qui auraient été affectés à chaque sujet s'ils n'avaient pas été ex-æquo (par exemple si entre le rang 4 et 9 on trouve 4 ex-aequos, le rang pour ces quatre observations sera 5+6+7+8 divisé par 4 soit le rang 6.5). Si le nombre d'ex-æquos est important, il faut toutefois corriger le coefficient de Spearman (cf. le calcul de la correction : Rakotomalala, 2015). Attention : si on utilise la formule de Bravais-Pearson sur les rangs (en affectant toujours le rang moyen pour les ex-æquos), il n'y a pas besoin de corriger (c'est plus simple !).

■Ce coefficient peut permettre d'évaluer une liaison non linéaire à la différence du Bravais-Pearson, à condition que la liaison soit monotone. Lorsque cette fonction est non monotone, le rho de Spearman est inopérant (comme le coefficient de Bravais Pearson).

■Ce coefficient est plus "robuste" face à des poins aberrants. Dans l'exemple concernant le point aberrant proposé plus haut (figure B-4) la corrélation de Spearman (avec le point aberrant) passe à .36 (bien plus proche de la valeur observée sans ce point aberrant qui est de .32).