La mesure d'aplatissement (= degré de voussure) ou Kurtosis (du grec kurtos signifiant courbe ou arrondi) est une statistique descriptive (moment centré d'ordre 4*) mesurant l'aplatissement de la distribution ou ce qu'on appelle encore son degré de voussure ou parfois sa "kurtose".
Figure H.2 : Exemples de distributions ayant 3 degrés différents de voussure (kurtose)
Pour une distribution normale, la valeur de ce coefficient (moment centré d'ordre 4) est de 3 pour une distribution normale. En pratique, on utilise le plus souvent un coefficient corrigé G2 (kurtosis normalisé**). La valeur de ce coefficient est alors de 0 pour une distribution normale (courbe dite alors mésokurtique). Un coefficient d'aplatissement négatif indique une distribution plutôt aplatie (platykurtique) et un coefficient d'aplatissement positif, une distribution "pointue" (leptokurtique). La formule de calcul de ce coefficient d'aplatissement normalisé et non biaisé est :
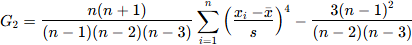
|
Avec : - n le nombre d'observations - xi le score observé pour l'observation i - x̄ et s la moyenne et écart-type non biaisés (***) |
--------------
(*) Pour ceux qui veulent savoir : Un moment d'ordre r est une moyenne des écarts par rapport à un réel "a" élevés à une puissance "r", r étant un entier naturel. La moyenne et la variance sont des moments d'ordre 1 et 2. Le skewness et le kurtosis des moments d'ordre 3 et 4 (facile à comprendre si on inspecte les formules de calcul de ces indices).
(**) Le terme excès d'aplatissement dérivé de "kurtosis excess" en anglais est utilisé parfois à la place de kurtosis normalisé mais il est ambigu car un excès d'aplatissement positif est une courbe leptokurtique (distribution pointue) et un excès d'aplatissement négatif à une courbe platykurtique (distribution aplatie).
(***) un estimateur non biaisé pour la moyenne et l'écart-type s'obtient en remplaçant n par n-1 dans les formules de la moyenne et de l'écart-type