Scores z

La note z (le score z ou encore score standard) correspond à l'expression d'un écart à la moyenne exprimé en fraction d'écart-type. Pour une distribution de notes de moyenne m et d'écart-type σ, la note z correspondant au score x se calcule facilement et correspond à :

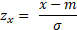
Propriétés

→La moyenne des notes z est égal à 0 et l'écart-type est égal à 1

→Ce score permet de répondre à la question : de combien de fraction d'écart-type s'éloigne-t-on de la moyenne ?

→ La transformation en score z est une transformation linéaire. Elle ne change une distribution bimodale ou asymétrique en distribution normale ! La "forme" de la distribution est conservée.

→L'étalonnage a pour objectif de donner un sens à la mesure. Cet étalonnage, pour qu'il ait un sens, ne devrait être utilisé que si les scores bruts se distribuent normalement ou quasi-normalement (il est toujours possible de transformer un score en note z, mais ce score n'a de sens que si la distribution est normale). Malheureusement beaucoup de psychologues semblent avoir oublié cette règle (même dans certains manuels de tests publiés). Si cette règle n'est pas respectée, l'interprétation du score est complexe car il doit prendre en compte  l'importance et la nature de l’asymétrie de la distribution.

→Si la distribution initiale suit une loi normale (ce qui devrait être le cas pour que cette transformation soit intéressante) il est facile de connaître les probabilités d'avoir un score supérieur ou inférieur au score z observée en utilisant une table de la loi normale. Un calculateur est aussi à votre disposition. Certaines de ces valeurs sont fréquemment utilisées en psychologie et méritent d'être connues. Par exemples:

oLa presque totalité des scores z (99,7%) se trouvent entre -3 et +3. 

o95% des scores se trouvent entre -1.96 et +1.96.

oUne note de 1,96 signifie que l'on est à 1,96 écart-type au dessus de la moyenne (et donc que seul 2,5% des personnes auraient un score plus élevé).  

L'intérêt du z score. 

Comme pour tous les scores étalonnés les notes z ont du sens contrairement à un score brut. Ils expriment une distance par rapport à la moyenne des scores d'un groupe dans une unité (fraction d'écart-type) comparable quelle que soit la mesure. Il faut être prudent cependant : la distribution des notes brutes doit être normale ou a minima symétrique et unimodale pour que ces comparaisons aient du sens.

Remarques

•Le QIstandard  aurait pu s'exprimer facilement en note z. En effet l'écart-type du QI est 15, la moyenne 100, donc un QI de 85 correspond à une note z de (85-100)/15 = -1

•L’asymétrie même modérée d'une distribution comme une distribution leptokurtique ou platykurtique modérée, impacte le taux de faux positifs (Crawford & Garthwaite, 2005). C'est la raison pour laquelle l'utilisation d'un score z lorsque la distribution n'est pas normale n'est pas recommandée. Des exemples significatifs sont données par  Mathilde Muneaux (2018) dans son "Petit Guide de Psychométrie Clinique à l’Usage des Praticiens" pages 61 à 65.