La représentation graphique consiste à représenter dans l'espace des facteurs (composantes), les variables. Elle est donc la "transcription" graphique partielle du tableau des saturations. Le principe de cette représentation est simple mais les représentations graphiques permettent de visualiser au plus 2 ou 3 facteurs (pour les espaces à plus de 3 dimensions, la représentation graphique simple est impossible). Dans ce cas (le plus fréquent), pour interpréter les résultats, on utilise donc directement la table des saturations et très peu les représentations graphiques.
ILLUSTRATION SIMPLIFIEE
Soit une table de saturation simple avec deux facteurs et 4 variables (adapté de Reuchlin, 1976) :
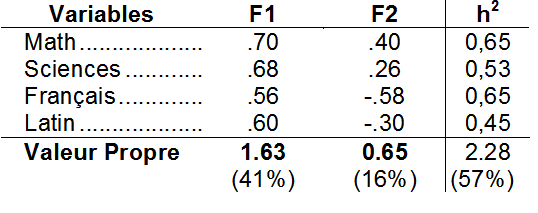
La représentation graphique va consister à représenter dans l'espace des facteurs (axes F1 et axes F2) les variables par des vecteurs ayant pour coordonnées les saturations.
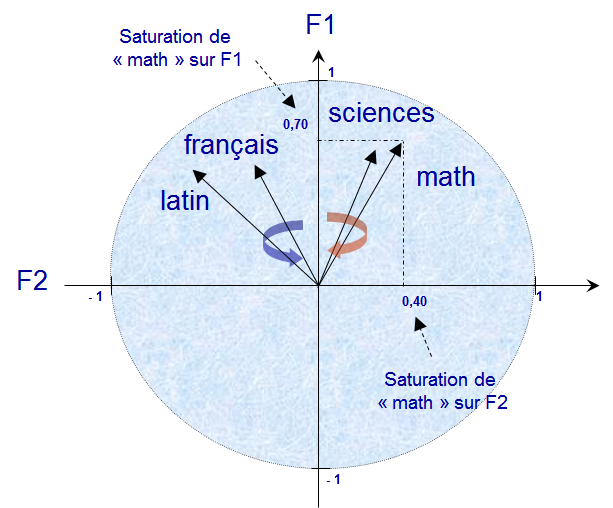
|
Figure H.8. Représentation graphique des variables dans l'espace des 2 premiers facteurs avant rotation. |
Cette représentation permet de repérer qu'il y a deux groupes de vecteurs mais pour lire correctement le graphique il faut avoir compris que :
▪Plus un vecteur est proche d'un axe, plus il est expliqué (associé) à la composante correspondant à cet axe.
▪La longueur du vecteur (qui correspond à la norme du vecteur) est en relation avec la quantité de variance de la variable (vecteur) expliqué par les 2 composantes. Plus le vecteur est grand plus il est expliqué par les deux composantes. En fait le carré de la norme du vecteur est la quantité de variance expliquée par les facteurs (composantes) puisque c'est la somme des carrés des saturations (théorème de Pythagore tout simplement !)
▪Cette norme (longueur du vecteur) ne peut dépasser 1 (une variable ne peut être expliquée à plus de 100%) et tous les vecteurs s'inscrivent dans un cercle de rayon 1 (cercle bleu sur le graphique)
Remarque : l'exemple précédent est une représentation avant rotation. La rotation VARIMAX va consister à rechercher deux nouveaux axes orthogonaux qui passent au plus près (pour chacun d'eux) d'un des groupes de vecteurs.
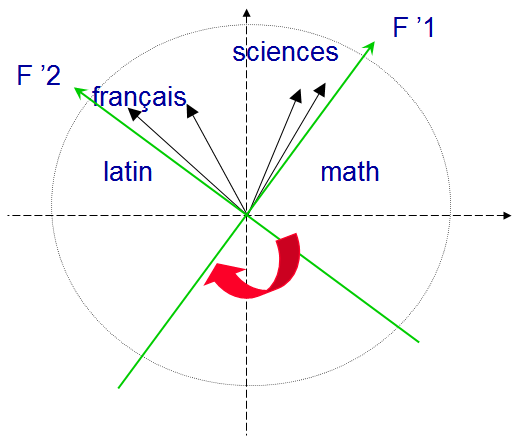
|
Figure H.4. Représentation graphique des variables dans l'espace des 2 premiers facteurs après rotation VARIMAX |
Une rotation oblique aurait conduit à faire passer les axes au "centre" de chaque groupe de vecteur. Dans ce cas les axes n'étaient plus orthogonaux et les facteurs corrélaient entre eux. Cette solution aurait traduit le fait que toutes les variables après rotation VARIMAX se situent dans le même quadrant, et qu'il existe une corrélation entre toutes ces variables.