Stratification

La méthode probabiliste stricte repose uniquement sur le hasard, hasard qui parfois "fait mal les choses" (biais d'échantillonnage par sur-représentativité d'un sous groupe). Pour contrôler la représentativité de l'échantillon, on peut utiliser la méthode de stratification.

Cette méthode nécessite d'avoir des informations sur chaque individu (par exemple : sexe, âge, profession, etc.) et la fréquence de ces caractères dans la population. On reproduit alors dans l'échantillon les caractéristiques  de la population de référence, en tirant au hasard les individus non plus dans la population globale mais dans des strates (sous groupes) définies par les variables retenues pour caractériser la population.

Par exemple, si dans une  population il y a 52% de femmes et 48% d'hommes et que l'on veut prendre en compte uniquement cette caractéristique, on échantillonne au hasard (méthode probabiliste stricte) parmi les femmes (première strate) puis parmi les hommes (seconde strate) un nombre d'individus de façon à ce que cette proportion soit respectée dans l'échantillon (52% seront des femmes et 48% des hommes). On peut stratifier un échantillon sur plusieurs caractères considérés conjointement (sexe et habitat et profession par exemple). Les unités (personnes ici) sont ensuite tirées au hasard à l'intérieur des strates ainsi définies.

Remarques :

•Avec cette méthode on a autant de tirage simple au hasard (bases de sondage) que de strates.

•Cette méthode présente un intérêt  si le critère de stratification est en relation avec l'objet d'étude (il est par exemple totalement inutile de faire des strates en fonction de la couleur des yeux si l'on construit un test d'intelligence). Les variables prises en compte pour constituer les strates constituent, si l'on prend en compte l'objet d'étude pour constituer les strates, un modèle (partiel) de la population parente.

•Cette méthode est toujours une méthode probabiliste. Chaque individu de la population parente possède la même probabilité de faire partie de l'échantillon. Elle nécessite toujours une liste exhaustive de la population parente.

•Si les variables à la base des strates sont biens choisies, cette méthode permet de diminuer les risques de biais d'échantillonnage (donc permet en principe, pour le même risque d'erreur, de diminuer la taille de l'échantillon). La qualité des strates détermine en partie la représentativité de l'échantillon.

Exemple pratique :

On souhaite réaliser une étude sur les projets professionnels d'étudiants inscrits dans une université Française (par exemple l'université Savoie Mont Blanc). Pour construire l'échantillon, les auteurs de l'étude observent que les étudiants sont réparties par groupe disciplinaires dans des Unités de Formation et de recherche (UFR) et les projets professionnels peuvent être très différents. Par ailleurs ils pensent qu'un autre facteur pourrait impacter les résultats : le niveau d'étude (premier ou second cycle). Ayant accès à la base de données de l'université, il vont constituer des strates en fonction de ces deux critères et sélectionner au hasard des étudiants à l'intérieur de ces strates. Le nombre d'étudiants pris au hasard dans chacune des strates sera fixé en fonction de la taille de l'échantillon total souhaité mais en respectant les proportions observées dans chacune des strates pour cette université.

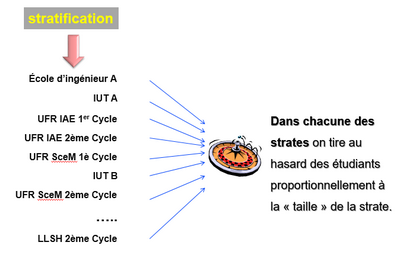
Figure D.1 : Illustration d'un échantillonnage par stratification.