Indice de Findley (d-index)

Principe. Les compétences réelles des personnes étant inconnues lors de l'élaboration d'un test on détermine l'indice de discriminabilité d'un item (d-index) de la façon suivante :

○dans l'échantillon, on construit deux groupes de personnes :  les performants (le sous-groupe des 27% de personnes ayant les scores les plus élevés sur l'ensemble de l'épreuve) et les « peu performantes » (le sous-groupe des 27% de personnes ayant les scores les moins élevés sur l'ensemble de l'épreuve).

○Pour chaque item, et dans chacun des sous groupes on calcule un p-index.

○On calcule le d-index qui est la différence entre les  p-index de ces deux sous-groupes (p-index des "plus performants" moins le p-index des "peu performants".

Plus l'indice (le d-index) est proche de 1, plus l'item discrimine les personnes. Plus cet indice est proche de 0, moins il différencie (dans ce cas on ne retient pas l'item). Si l'indice est négatif cela signifie que les "plus performants" dans l'échantillon réussissent moins cet item que les "peu performants". Un item ayant un d-index faible ou négatif nuit donc à l'homogénéité de l'épreuve et on l'élimine. 

Exemple.  Soit l'administration d'un test composé de 9 items. On calcule le score total au test (nombre de bonnes réponses). Pour chaque item on calcule la proportion de sujets ayant réussi l'item parmi les 27% des meilleurs score au test (p1) et la proportion de sujets ayant réussi parmi les 27% les moins efficaces au test (p2). Remarque : p1 et p2 sont des indices de difficultés pour chaque sous groupe (cf. tableau ci-dessous). Le d-index est simplement la différence entre p1 et p2.

I5, I6 et dans une moindre mesure I4 nuisent à l'homogénéité de l'instrument.

Attention : Si potentiellement, le d-index peut varier entre -1 et +1, sa valeur maximale pour un item i  est directement dépendant du  p-index:

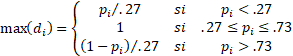
avec : pi le p-index de l'item i

Cette formule signifie qu'un item très difficile (p-index inférieur ou très inférieur à .27) ne peut avoir qu'un d-index peu élevé. En effet si 5% des personnes réussissent un item et que ces 5% sont réellement les meilleurs, p1 sera égal à 5/27 donc 0.185 et p2  sera égal à 0 (si on prend la notation du tableau ci-dessus). Le d-index sera alors de 0.185 (ce qui correspond bien à la valeur maximale possible donnée par la formule  soit 0.05 * 0.27). Le d-index parait  donc peu élevé mais on doit tenir compte que c'est le maximum possible au vu de la valeur du p-index global. 

De la même façon, si un item est très facile (p-index supérieur ou très supérieur à .73), le d-index ne peut être que faible. On doit donc tenir compte du p-index pour calculer le d-index maximum possible et comparer avec le d-index observé (pour chaque item). 

Pour aller plus loin...

Une variante de l'indice de Findley est l'indice B de "discrimination au seuil de maîtrise" (Brennan, 1972) que l'on peut utiliser pour des tests de connaissances (le plus souvent des tests scolaires). Pour calculer cet indice, on se fixe un seuil (niveau de maîtrise du contenu, par exemple réussite à 80% des items) et on constitue 2 groupes, ceux qui réussissent à 80% ou plus et tous les autres. Cet indice se calcule alors comme l'indice de Findley (indice de difficulté pour ceux qui maîtrisent moins indice de difficulté calculé sur ceux qui ne maîtrisent pas). A nouveau cet indice dépend du niveau de difficulté des items et du seuil de maîtrise que l'on se fixe.