Coefficient de corrélation bisérial de point
Une autre façon d'envisager la relation entre le score à un item et le score au test consiste à utiliser le coefficient de corrélation bisérial de point (rpbis) :
|
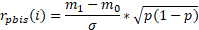
avec m1 : la moyenne observée à l'épreuve pour ceux qui ont réussi l'item i m0 : la moyenne observée à l'épreuve pour ceux qui ont échoué l'item i σ : l'écart-type des scores p : la proportion des personnes ayant réussi l'item i |
Remarques :
▪En général, pour étudier les items on utilise un coefficient corrigé en utilisant un score total calculé sans tenir compte de l'item évalué.
▪Il s'agit d'une corrélation item-test. Un item discrimine correctement un test si il existe une corrélation positive entre le score à l'item et le score au test. Ce coefficient peut varier (comme le coefficient de corrélation de Pearson) entre -1 et +1. Il faut savoir cependant que ces valeurs maximales ne peuvent être observées que si la proportion des personnes ayant réussi (p) l'item est de .50.
▪La formule du coefficient de corrélation bisérial de point est simplement une formule qui permet de simplifier les calculs. Mais on peut appliquer la formule de Bravais Pearson (avec des 1 et 0 pour la variable dichotomique) et on obtient le même résultat.
▪L'utilisation du coefficient bisérial de point est celui qui est le plus souvent utilisé car les items sont souvent dichotomiques. D'autres coefficients de corrélations peuvent cependant être utilisés.