La correction pour atténuation (parfois appelé coefficient de désatténuation) dans l'analyse de la force d'une corrélation est une procédure pour tenir compte de l'erreur de mesure.
En effet la corrélation entre deux variables dépend directement de l'erreur de mesure. Plus la variance d'une variable correspond à de la variance d'erreur (i.e. plus les différences observées ont pour origine des facteurs aléatoires non contrôlés ou contrôlables), plus la corrélation avec une autre variable sera faible (Spearman, 1904a). La corrélation est une mesure de la part de variance commune à deux tests et seule la variance vraie peut être commune. Si deux mesures sont totalement aléatoires (c-à-d uniquement de l'erreur de mesure) les deux mesures ne corréleront pas. En fait, la variance commune maximum possible est égale au produit des fidélités et la corrélation maximum possible est donc égale à la racine carrée du produit des fidélités (le coefficient de fidélité est une évaluation de la part de variance vraie).
La corrélation corrigée pour atténuation (cf. formule ci-dessous), en rapportant la corrélation observée (racine carrée de la variance commune) à la corrélation maximum possible, permet de tenir compte de cette erreur de mesure. On mesure ainsi la relation entre les scores vrais (relation qui nous intéresse directement).
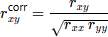
|
avec : rxx est la fidélité du test x ryy est la fidélité du test y |
A savoir
•Cette correction pour atténuation est particulièrement utilisée lors de la recherche de preuves de la validité des tests (et plus particulièrement la validité empirique qui s'appuie sur la corrélation observée entre tests et critères).
•La corrélation maximum entre deux mesures est comprise entre les valeurs des deux fidélités. Plus précisément, si deux tests ont une fidélité égale respectivement à .70 et .80, la corrélation entre ces deux tests sera égale au maximum à la racine carrée de .70 * .80 soit r(max) = .748
•Plus la fidélité est forte, plus la corrélation (sans correction pour atténuation) avec un autre test ou un critère pourra être forte. Une fidélité faible minimise à l'inverse les corrélations.
•Une faible corrélation entre deux tests peut donc avoir pour origine une fidélité faible de l'un ou des deux tests.