Centiles - Percentiles

Les centiles (ou percentiles qui est un anglicisme) sont les valeurs d'une variable qui partitionnent la distribution des scores ordonnés en 100 intervalles contenant le même nombre de données (quantiles d'ordre 100). Il y a donc 99 centiles (99 valeurs de la variable correspondant chacune à un centile).

Déterminer les centiles d'une série de valeur :

La méthode qui semble la plus utilisée est la suivante (Nearest Rank method).

1.Trier les valeurs par ordre croissant : X1 < X2 < … < Xi < … Xn-1 < Xn

2.Le centile P est la valeur du kième élément avec k = P* n / 100 (la valeur de k est arrondie au nombre entier supérieur le plus proche).

La méthode recommandée par le National Institute of Standards and Technology (NIST).

1.Le rang k est calculé de la façon suivante : k = P*(n+1)/100.

2.La valeur k est ensuite séparée en deux valeurs, sa partie entière (e) et sa partie décimale (d). Le centile est ensuite déterminé selon la règle suivante (avec vi la ième valeur observée dans la série ordonnée) :

®si e=0 alors  le centile est v1 (la première valeur observée)

®si e>=n alors  le centile est vn (la dernière valeur observée)

®sinon le centile se calcule par interpolation linéaire et est égale à : ve + d*(ve+1 - ve)

Une méthode alternative (toujours recommandée par le NIST) :  similaire à la précédente, sauf que la valeur k est égale à 1 + P*(n-1)/100

Remarques :

■Le terme de centile (percentile) a été utilisé pour la première fois par Francis Galton à la fin du 19ème siècle.

■Les méthodes de calcul des centiles peuvent être différentes d'un logiciel à l'autre et donner des résultats légèrement différents.

■Les centiles doivent être différenciés des rangs centiles (ou rangs percentiles). Un centile est une valeur de la variable pour un rang centile entier (1 à 99), alors que le rang centile est le rang associé à une valeur de la variable.

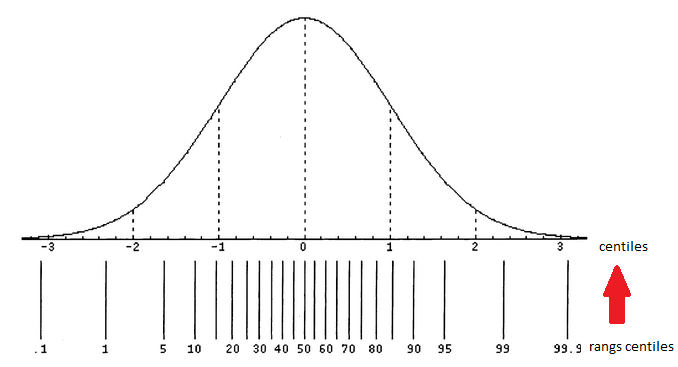
■Il faut faire attention à l'interprétation des centiles et des rangs centiles car on a tendance à sur-interpréter ou sous-interpréter les valeurs observées. (cf. à ce sujet, Bowman, 2002). Les centiles ne sont pas à équidistance les uns des autres lorsque la distribution n'est pas "rectangulaire" pour une échelle d'intervalle (cf. ci-dessous les rangs centiles associés à la loi normale).