La loi normale

Lorsqu'une série de mesure subit l'influence de sources aléatoires alors les caractéristiques de cette série répondent à la loi normale (théorème central limite). 

La loi normale est la plus connue des lois de probabilité. Sa fonction de densité a une forme simple (courbe en cloche) et est symétrique et presque toutes les valeurs se trouvent entre moins trois écarts-types et plus trois écarts-types de la moyenne (plus de 99%). On notera aussi que 95% des valeurs se trouvent à ± 1.96 écart type de la moyenne).

Définition formelle. 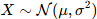 est définie sur R (ensemble des réels) par  : 

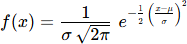
La représentation graphique est la suivante :

Figure H.7 : Distribution normale et ses 2 paramètres (m et σ)

Remarques

▪Cette courbe, caractéristique de la loi normale, est aussi appelée courbe de Gauss en l'honneur de Karl Friederich Gauss (1777-1855). La fonction associée a aussi pour nom loi de Laplace-Gauss (Pierre Simon Laplace, 1749-1827, étant un autre grand mathématicien, astronome, physicien et philosophe).

▪Le théorème central limite énonce, dans sa forme générale, que sous certaines conditions,  notamment l’existence de moyennes finies et de variances finies et non nulles, la moyenne d’un grand nombre de variables aléatoires indépendantes* et identiquement distribuées tend vers une loi normale, quelle que soit leur distribution d’origine.

(*) Deux variables aléatoires sont dites indépendantes quand le résultat de l'une n'influence pas le résultat de l'autre.