Taille des échantillons

Définir la taille d'un échantillon est complexe et différents facteurs affectent la détermination du nombre de personnes devant appartenir à l'échantillon (taille d'échantillon). Il existe  différentes formules et techniques mais toutes ces méthodes montre que l'on doit prend en compte :

®Le degré de certitude ou le niveau de confiance que l'on veut avoir (intervalle de confiance) dans les résultats. Plus on souhaite avoir une marge d'erreur faible plus l'échantillon devra être important (si la méthode d'échantillonnage est correcte).

®la prévalence estimée de la variable étudiée (exemple pour une question en oui-non, la fréquence attendue des oui et non) ou pour d'autres types de mesure la dispersion des valeurs autour de l'indice de tendance centrale.

®la méthode d'échantillonnage (plan d'échantillonnage) détermine aussi (toute chose étant égale par ailleurs) la taille d'un échantillon. Par exemple la méthode par stratification assure a priori une meilleure représentativité que d'autres méthodes d'échantillonnage. Dans ce cas, la taille de l'échantillon peut être moins importante qu'avec une autre méthode (pour le même degré de précision).

®la taille de la population parente. Ce facteur qui parait évident et qui doit être pris en compte lorsque la population de référence à des faibles effectifs, devient de moins en moins important lorsque l'effectif de la population parente devient très important. Son importance est donc relative (cf. pour aller plus loin... ci dessous).

Remarques

■Si la méthode d'échantillonnage est incorrecte, augmenter de façon importante la taille de l'échantillon n'apporte aucune garantie sur la validité ou la représentativité de l'échantillon.

Les exemples les plus fameux dans ce domaine concernent les premiers sondages et enquêtes pré-électorales effectués aux USA. Il est rapporté plus particulièrement celui concernant l'élection présidentielle opposant Roosevelt à Landon. Un journal a effectué un sondage auprès de 3 millions de personnes et donnait Landon gagnant, or, Gallup, avec un sondage auprès de 4500 personnes, donnait avec raison Roosevelt gagnant. Le biais du premier sondage était simple à repérer : l'enquête avait été faite par téléphone auprès des abonnés du journal, et les personnes interrogées n'étaient pas représentatives de la population américaine même si elles étaient 665 fois plus nombreuses. Lorsque qu'un auteur met en avant la "grande taille" ou l'importance de son échantillon, il faut toujours regarder la méthode d'échantillonnage.

■La qualité de la mesure issue d'un échantillon n'est pas directement proportionnelle à la taille de l'échantillon. Il ne suffit pas de doubler la taille d'un  échantillon pour doubler la qualité de la mesure. Schématiquement, pour multiplier par 2 la qualité de la mesure, il faut par exemple multiplier par 4 la taille de l'échantillon.

■En théorie, les méthodes de calcul de la taille d'échantillon ne s'appliquent que sur les échantillons obtenus par des méthodes probabilistes. En pratique, ces méthodes de calcul sont quand même utilisées pour les méthodes non probabilistes et corrigées (éventuellement). Selon la méthode d'échantillonnage choisie les instituts de sondage multiplient les résultats par un coefficient prenant en compte les caractéristiques du plan d'échantillonnage. Par exemple, pour une méthode par grappe, ils peuvent doubler la taille d'échantillonnage nécessaire pour une méthode probabiliste stricte.

Pour aller plus loin ....

Illustration de l'effet des différentes facteurs dans la détermination de la taille d'un échantillon (par simulation)

Pour cette simulation, qui est la uniquement pour illustrer des effets classiques, nous nous plaçons dans un cadre simple, celui d'une enquête qui cherche à savoir si dans une population on préfère le produit A ou le produit B. Pour calculer la taille de l'échantillon (population parente finie), la formule utilisée est  :

Cette formule, va nous permettre d'illustrer les effets des différentes variables (taille de l'échantillon, de la population parente, etc.) sur le degré de confiance dans les résultats. Vous pouvez aussi avec un tableur faire d'autres simulations. En fait, le principe est de faire varier, un paramètre et on regarde l'effet sur un autre paramètre (en laissant les autres paramètres constants).

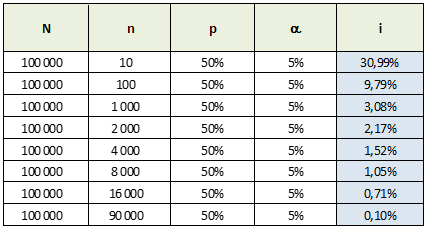
Simulation 1 : pour une taille de population donnée (N), plus l'échantillon est grand (n), meilleure est la précision  (fourchette i diminue)

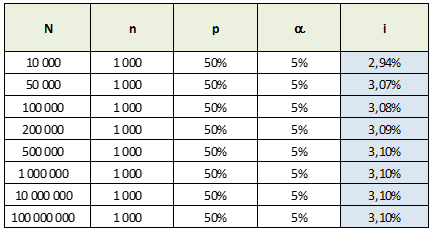
Simulation 2 : la taille de la population parente (N) a une importance toute relative dans le degré de confiance (i.e précision, fourchette i) à taille d'échantillon suffisante (n=1000). En fait, avec 1000 individus, la précision du résultat est similaire pour une population parente de 200 000 individus et pour une population parente de 100 000 000 individus !

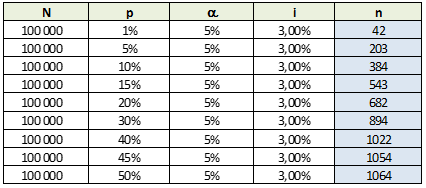
Simulation 3 : pour un degré de précision fixé (ici  i= 3%), la taille de l'échantillon (n) pour une population de référence constante (N=100 000) dépend de la proportion de choix A (p) dans la population parente. En fait, la taille de l'échantillon est maximum pour p=50% (donc quand la dispersion est maximum). Comme avant une étude on ne connaît pas p, on se met toujours dans ce cadre pour calculer la taille de l'échantillon.