Paramètre de discrimination

C'est Birnbaum qui introduit (dans les modèles à deux paramètres), le deuxième paramètre correspondant au niveau de discrimination, que l'on appelle paramètre α. La discrimination de l'item (c'est à dire sa propension à bien discriminer les individus les uns des autres) est représentée par la pente de la CCI (tangente au point d'inflexion de la CCI). Celle-ci peut être plus ou moins inclinée. Plus la pente est "abrupte" (tend à être parallèle à l'axe Y), plus l'item est discriminant et inversement.

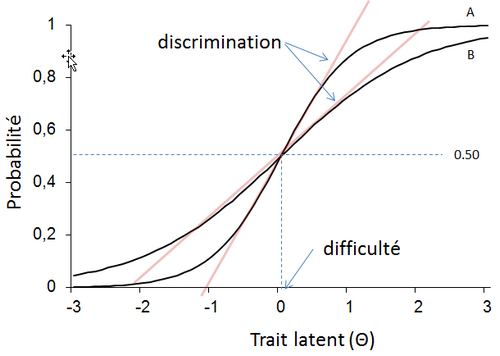
Par exemple, ci-dessous, les items ont la même difficulté et ne sont pas aussi discriminants. Les pentes des courbes représentées sont clairement différentes. L'item A est plus discriminant.

Comprendre : un item correspondant à un niveau l sur le trait latent (ϴ) est discriminant si la probabilité de réussite est minimum lorsque la position sur le trait latent est inférieur à l et maximum lorsque la valeur sur le trait latent est supérieur à l. En fait, l'intervalle de valeur sur ϴ pour que la probabilité de réussite passe de de son minima à son maxima doit être minimum si l'on veut que l'item soit discriminant (cf. figure E.6).

Remarque :  En règle général la valeur ai de α (paramètre de discrimination) est positive et varie entre 0 et 2 (2 étant une valeur élevée). Plus cette valeur est élevée, plus l'item est discriminant. Si la valeur de la pente était négative cela signifierait que la probabilité de réussir l'item diminue lorsque la compétence augmente (absurde, la fonction serait monotone décroissante).