Erreur standard de mesure et TCT

L’Erreur Standard de Mesure (ESM) plus souvent appelé SEM (notation anglo-saxonne) se détermine à partir du coefficient de fidélité (rappel : le coefficient de fidélité représente la part de variance correspondant à des différences vraies, non aléatoires, entre les personnes). Soit sx l'écart-type des scores dans la population et rxx le coefficient de fidélité, on calcule le ESM à partir de la formule suivante :

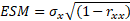
Dans l'absolu, l'ESM  correspond à l'écart-type des scores observés sur des mesures parallèles répétées pour une personne ayant une note "vraie" fixe et invariable.

Remarques :

■Plus la fidélité d'un test est bonne, plus l'ESM est petit. L'ESM varie en fonction du coefficient de fidélité.

■L'ESM permet de relativiser l'importance accordée au score (cf. intervalle de confiance)

■L'erreur standard de mesure ne doit pas être confondue avec l'écart-type (racine carrée de la variance) et l'erreur-type qui est, pour un échantillon donné, l'écart-type divisé par la racine carré du nombre de sujet (cf. tableau ci-dessous)

■Dans certaine traduction française l'ESM est appelé erreur type de mesure.

avec : n le nombre d'individu, m la moyenne et rxx le coefficient de fidélité.