Erreur standard de mesure et MRI (C-ESM)

Dans le cadre des modèles de réponse à l'item (MRI), l'erreur standard de mesure (ESM) peut être calculée pour chaque valeur du trait latent à partir de la courbe d'information I(θ). Elle sera d'autant plus faible que l'information apportée est élevée. Cette erreur de mesure, pour chaque valeur de thêta, est égale à 1 sur la racine carré de l'information apportée :

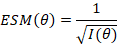
I(θ) est l'information apportée pour la valeur thêta.

Contrairement à la théorie classique des tests, l'erreur de mesure varie donc en fonction du trait latent (on parle d'erreur standard de mesure conditionnelle ou C-ESM). On représente souvent sur un même graphique la courbe d'information et l'erreur standard de mesure (cf. ci-dessous). On notera que dans ce type de représentation graphique, les échelles relatives à ces deux courbes ne sont pas les mêmes.