La méthode utilisée est la même que celle présentée dans le cadre du calcul de l'intervalle de confiance d'un score observé. Cette fois on utilise l'erreur standard de mesure de la différence (ESmdif). Dans la théorie classique des tests, les erreurs ne sont pas corrélées. On peut en déduire que l'ESM de la différence (ESMdiff) se calcule à partir de l'erreur standard de mesure de l'épreuve 1 (ESM1) et l'erreur standard de mesure de l'épreuve 2 (ESM2) :
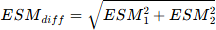
Sachant que pour comparer deux scores il est nécessaire que les échelles de mesures soient semblables, la formule précédente peut-être remplacée par une formule équivalente par :
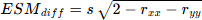
|
avec : s = l'écart-type identique des deux épreuves (x et y) rxx et ryy : la fidélité (rxx et ryy) des deux épreuves x et y |
Pour dire que la différence entre 2 scores est suffisamment importante on s'appuie sur le fait que la distribution du score de différence (sous l'hypothèse d'absence de différence) suit une loi normale de moyenne 0 et ayant pour écart-type ESMdiff. Comme pour le calcul de l'intervalle de confiance d'un score observé, on fixe alors un seuil (5% ou encore 1%) et on lit dans une table de la loi normale la valeur u. On multiplie u par le ESMdiff pour connaître les deux bornes de l'intervalle de confiance. Si, la différence observée est à l'extérieur de cet intervalle, on peut conclure que la différence entre less deux scores est statistiquement significative, c’est-à-dire qu’elle dépasse ce qu’on pourrait attendre du simple fait de l’erreur de mesure.
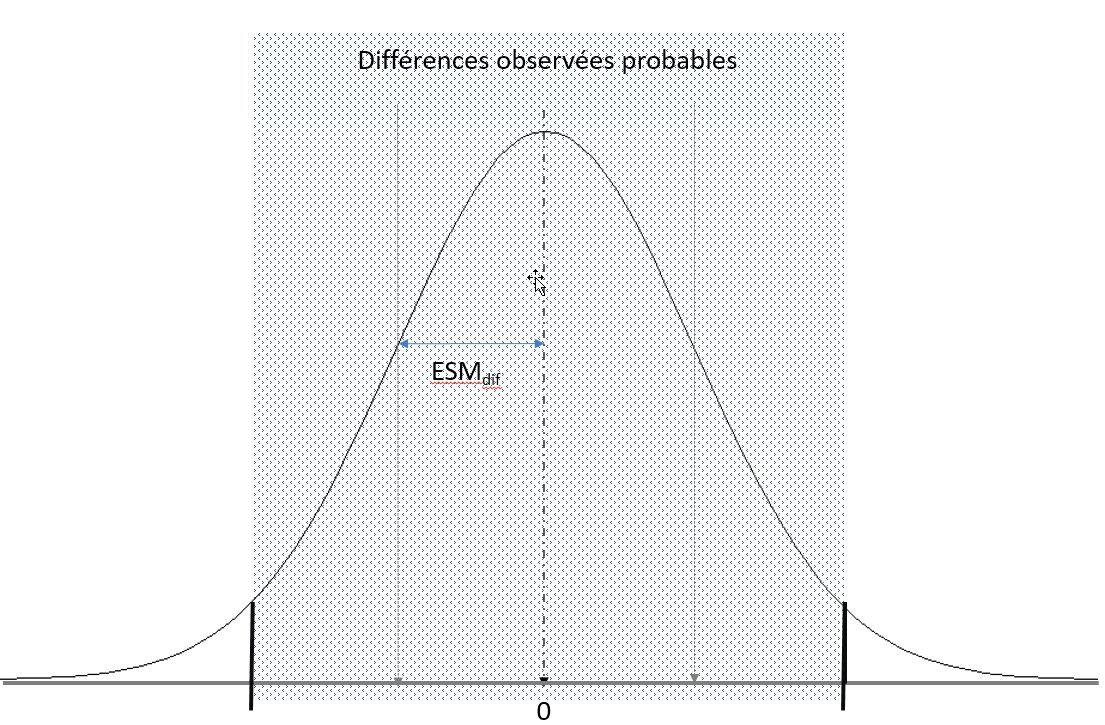
[- u * ESM ; + u * ESM]
avec u la valeur lue dans la table de la loi normale