Stanine

Le terme « stanine » trouve son origine dans l’expression anglaise standard nine (échelle standardisée en neuf échelons).  Cette échelle repose sur une transformation des scores bruts en neuf catégories correspondant à des intervalles de la distribution normale. Elle est bornée entre 1 et 9, avec une moyenne théorique de 5 et un écart-type d’environ 2 (m=5, s≈2, min=1 ; max = 9).  Cette échelle permet de représenter la position relative d’un individu au sein de la population de référence sur une échelle discrète et symétrique. Pour construire l’échelle en stanines, deux approches peuvent être envisagées selon la nature de la distribution :

Méthode 1 : la distribution est normale ou quasi-normale. 

La démarche est identique à celle d'une échelle réduite en 9 classes (l'étendu de la classe est de 0.5 écart-type). La formule suivante peut être utilisée (pour une distribution de moyenne m et d'écart-type s) :

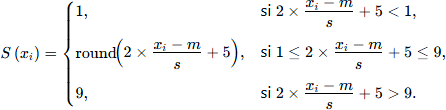
 L'expression (xi-m)/s dans la formule précédente correspond à une transformation linéaire du score initial en score z. Cette valeur est ensuite doublée puis on ajoute 5. Le score est arrondi et les valeurs supérieures à 9 sont ramenées à 9 et celles inférieures à 1 sont ramenées à 1.  

Méthode 2 : la distribution n'est pas une distribution normale.

La procédure est similaire à celle utilisée pour une  une échelle normalisée. A partir des scores observés auprès de l'échantillon de standardisation, l'étalonnage de l'épreuve va consister à associer chaque score possible à une classe (un échelon de l'échelle). Les scores sont ordonnés du plus petit au plus grand. Les 4% premiers scores sont associés à la catégorie 1, les 7% suivant à la catégorie 2, etc.. La table suivante vous indique les pourcentages.  

Interprétation

Avec le tableau, l'interprétation est simple. Par exemple un stanine de 3 signifie que l'on se situe autour d'1 écart-type en dessous de la moyenne (z autour de -1) et 73% des personnes (population de référence) ont un score en stanine supérieur. Un stanine de 6 correspond à une note z de autour de 0.5 et 23% ont un score supérieur.