Formule générale du RCI :
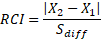
avec Sdiff l'écart-type associée à la différence entre deux scores
Pratique (un outils de calcul sera prochainement disponible dans les outils SCALP)
La formule la plus souvent utilisée pour calculer un indice de changement est celle basée sur les travaux de Jacobson et de ses collègues, en particulier Jacobson et Truax (1991) qui ont incorporé une correction de formule fournie par Christensen et Mendoza (1986). Elle nécessite de calculer écart-type associée à la différence observée entre deux passations (Sdiff) pour calculer un intervalle de confiance.
▸Calculs
⭢ calcul de l’erreur standard de mesure (ESM) avec ET comme écart type dans l’échantillon de standardisation et rxx la fidélité du test :
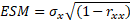
⭢Calcul de l'écart-type associée à la différence entre deux scores
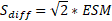
Pour conclure deux méthodes peuvent être utilisées (elles donnent le même résultat)
Méthode 1
⭢Calcul du RCI (formule ci-dessus)
⭢Comparer la valeur trouver au valeurs lues dans la table de la loi normale(test est bilatéral). Par exemple le changement est fiable au seuil que l'on se fixe (1%, 5%, 10%) si :
Pour un seul de 10% : RCI > = 1.64
Pour un seul de 5% : RCI > = 1.96
Pour un seul de 1% : RCI > = 2.58
Méthode 2
⭢Calcul de la valeur absolue de la différence (Δ) entre la passation 2 et la passation 1 : Xdiff = |X2-X1|
⭢Calcul d'une valeur seuil pour le score de différence entre la passation 2 et la passation 1
Pour un seuil de 10% ( p < .10) : Δ(90%) = 1.64 * Sdiff
Pour un seuil de 5% (p < .05) : Δ(90%) = 1.96 * Sdiff
Pour un seuil de 1% (p < .01) : ΔI(99%) = 2.58 * Sdiff
Remarques : en général on arrondit à l'entier le plus proche. Les valeurs (1,64, 1.96 et 2,58) sont les valeurs lues dans la table de la loi normale et le test est bilatéral.
⭢Décision : si le Xdiff est supérieur à la valeur seuil que l'on retient, le changement peut être considéré comme fiable au seuil que l'on s'est fixé. Dans le cas contraire la différence ne peut pas être considérée comme fiable (elle peut être due plus probablement à des facteurs aléatoires)
▸Remarques
•Dans ce contexte, le terme de changement fiable signifie que l'on peut affirmer de manière défendable que la différence observée sur les scores est plus importante que celui dû à la seule erreur de mesure.
•Un patient peut avoir un indice de changement fiable significatif, mais rester dans la zone cliniquement significative. Le RCI nous apprend rien sur le niveau de difficulté du patient, il nous renseigne sur l'existence d'un changement de niveau uniquement (présent vs absent).
Critiques, précautions et limites
Cet index, bien qu'il soit de plus en plus utilisé doit être cependant manipulé avec précaution en clinique. Il existe de nombreux articles dans la littérature soit pour l’amender, soit pour proposer des variantes plus ou moins complexes (Wise 2004, Speer 1992, Hageman & Arrindell, 1993). Il faut savoir en particulier (et entre autres) que :
•On doit vérifier l'effet de la pratique pour différent délai de passation. En effet cette formule de calcul du RCI suppose que dans l'intervalle de temps observé entre les deux mesures, il n'existe pas de modification du score ou que cette modification est faible dans l’échantillon de standardisation ou de référence.
•Parmi les nombreux débats concernant cet indice, le plus important repose sur le fait que cet indice fait intervenir le coefficient de fidélité. La question qui est posée et qui n’est pas résolue (Blampied, 2022) concerne la façon dont on estime la fidélité. En effet, même si très souvent la fidélité test-retest est recommandée, il n'est pas toujours évident qu'il s'agisse de la bonne solution. La corrélation r de Pearson du test-retest couramment rapportée est problématique car elle est insensible à l'erreur systématique entre les mesures répétées (Aldridge et al., 2017).
•Cette façon de calculer le RCI s'inscrit dans le cadre de la théorie classique des tests et suppose que l'erreur de mesure (donc la fidélité) ne varie pas en fonction du score observé ce qui est le plus souvent faux. Ord lorsque l'on travaille en clinique, les patients ont plus souvent des scores situés aux extrémités de la distribution !
La discussion sur le RCI est donc loin d'être close dans la littérature (Brooks, et al., 2011, Blampield, 2022) et l’utilisation de cet indice doit être fait avec précaution. Il s’agit d'un élément d'information à intégrer dans l’évaluation d’un effet. Il n’existe pas de rituel mécanique (Cohen, 1994) dont le recours nous dispenserait de la nécessité d'exercer notre jugement. C'est clairement le cas lors de l’utilisation d’un index de changement fiable.