Echelle réduite

Les échelles réduites sont utilisées uniquement  lorsque la distribution des notes brutes est normale ou quasi-normale. Les catégories de l'étalonnage vont être fondées sur des écarts à la moyenne.

Principe de construction.

Ces échelles sont faciles à mettre en œuvre. Le nombre de classes est habituellement impair (5, 7, 9, 11) et la classe centrale est centrée sur la moyenne. Les bornes d'une classe sont fixées ensuite en prenant comme étendue d'une classe. Cette étendue est déterminée de façon à ce que l’ensemble des classes couvre la distribution des scores et par convention, les valeurs utilisées sont le plus souvent :: 

Illustration

Soit une épreuve avec des scores possibles allant de 0 à 60, de moyenne 30 et d'écart-type de 10. L'objectif est de construire un étalonnage en 7 classes. Quatre étapes seront nécessaires :

1. Déterminer l'étendue des classes. Cette étendue, pour une échelle en 7 classes correspond à 0,67 * σ.  Cette étendue est donc de 0,67*10 = 6,7

2. Calculer les bornes de la classe centrale (classe 3) qui est centrée sur la moyenne par convention en psychométrie. Les bornes de cette classe sont donc à 6,7/2 soit 3,35 points de la moyenne de chaque coté (cf. schéma ci-dessous).

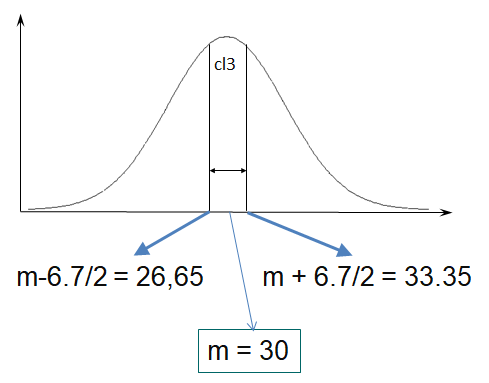
3. Il y a 7 classes donc 3 de chaque côté de la moyenne. Il suffit de progresser d'un pas de  6,7  à partir de chaque borne de la classe 3.

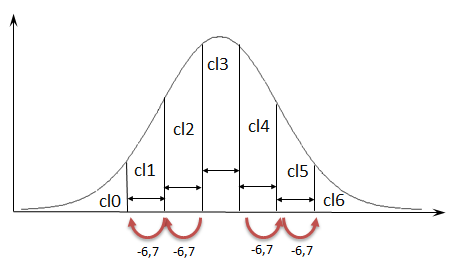
4. Cette règle a permis de calculer les bornes théoriques. Les bornes réelles (étalonnage), si les scores bruts sont des entiers vont remplacer ces bornes théoriques dans la table d'étalonnage. La règle est simple, pour la borne inférieure prendre l'entier supérieur de la borne inférieur théorique (exemple ⎡13.25⎤ =14) et pour la borne supérieur prendre l'entier inférieur de la borne théorique supérieure (par exemple : ⎣46.75⎦=46).

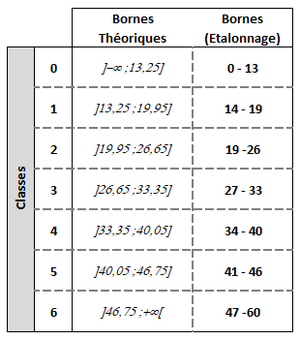
Remarques

▪Ce type d'étalonnage présente le grand avantage d'être aisé à établir mais nécessite que la distribution des scores bruts soit normale ou quasi-normale. 

▪Avant d'utiliser ce type d'échelle il faut réaliser  un test de normalité de la distribution (comme le test de Kolmogorov-Smirnov ou Lilliefors).

▪Si la distribution des données brutes n'est pas normale, les effectifs des diverses catégories varient irrégulièrement et surtout arbitrairement. 

▪L'étendu d'une classe est fixée par convention et peu varier d'une étude à l'autre mais les valeurs les plus fréquentes sont celles indiquées.