Echelle normalisée

Ces échelles sont une combinaison des deux types d'étalonnage précédents. Le principe général est de transformer les données en s'appuyant sur les caractéristiques de la courbe normale théorique et non pas sur la moyenne et l'écart-type des données brutes (comme pour les échelles réduites).

Principe de construction.

A.Transformer en échelle réduite une distribution normale théorique de moyenne 0 et d'écart-type 1. Comme pour une échelle réduite les classes seront donc construites autour de la moyenne.

B.Déterminer le pourcentage de personnes de l'échantillon qu'il doit y avoir dans chaque classe (ce qui est possible puisque l'on connaît la distribution de la loi normale théorique : Ν(µ=0, σ=1).

C.Appliquer la règle du quantilage pour déterminer les bornes de chaque classe.

Illustration

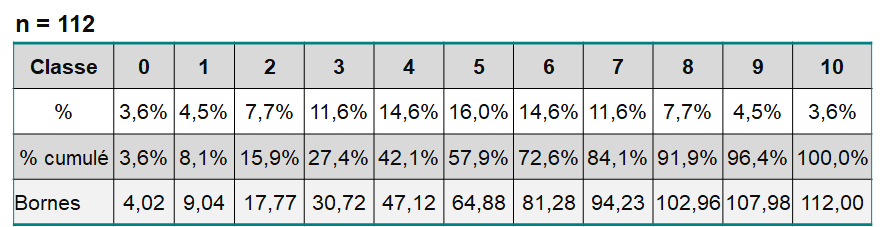
Dans une épreuve les scores bruts possibles vont de 20 à 80. Cette épreuve est administrée à 112 personnes représentatives des étudiants de psychologie de deuxième année. Construire, à partir de ces données, une échelle normalisée en 11 classes.

Étape 1.        Calcul des bornes pour distribution normale théorique de moyenne 0 et d'écart-type 1. L'étendu des classes par convention est de 0.40*sigma (11 classes). Les bornes sont (cf. méthode échelle réduite)  : 

-2.20 ; -1.80 ; -1.40 ; -1.00 ; -0.60 ; - 0.20 ; +0.20 ; +0.60 ; +1.00 ; +1.40 ; +1.80 ; + 2.20

Étape 2.        Calcule les pourcentage et le pourcentage cumulé de personnes se trouvant dans chacune des classes lorsque  la distribution est normale. On utilise pour cela une table de la loi normale.

Étape 3.        Procéder comme pour un quantilage mais avec les valeurs du tableau précédent. Les bornes ("pseudo-quantiles") sont calculées de la façon suivante :

Qi = n * %Fcumi

avec i Qi la borne supérieure de la classe i

n le nombre de sujet

%Fcumi le pourcentage cumulé de la classe i

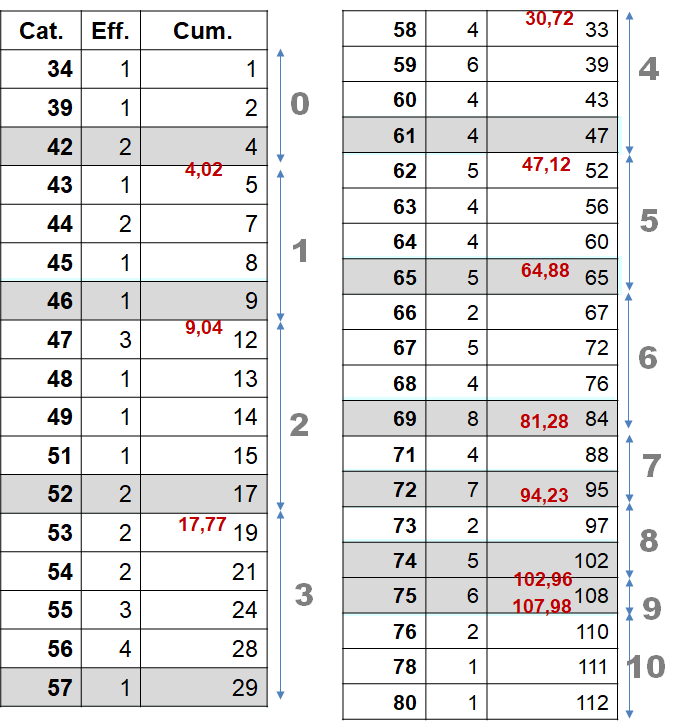
Étape 4.        Surligne dans le tableau des effectifs cumulés la classe avec l'effectif le plus proche de la borne calculée.

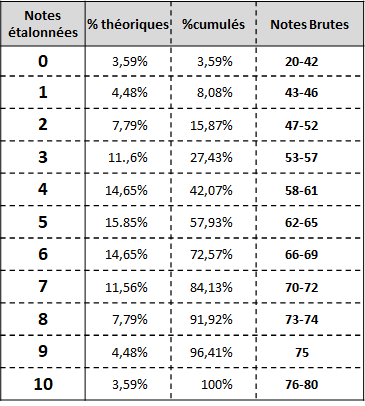
Étape 5.        Remplir la table d'étalonnage qui permet ensuite de convertir toutes les notes brutes en notes étalonnées. Toute les notes brutes apparaissent même celles qui ne sont pas observées dans l'échantillon (dans notre exemple le score minimum possible était 20).

Remarques

▪Les deux premières étapes de la procédure ne sont en fait jamais effectuées. En effet, il existe déjà des étalonnages en 11 classes et les pourcentages de chaque classe sont connues (les mêmes pour tous les étalonnages de ce type) et n'ont pas besoin d'être recalculées (sauf si l'on souhaite prendre une étendue  différente de celle habituellement utilisée).

▪Ce type d'étalonnage présente le grand avantage d'être aisé à établir et ne nécessite pas que la distribution des scores bruts soit normale. 

▪Si la distribution des scores bruts est normale une échelle normalisée donne les mêmes classes d'étalonnage qu'une échelle réduite.

▪Ce type d'étalonnage est très fréquent. Par exemple cette méthode est utilisée pour construire les notes standards en 19 classes dans les échelles de Weschler.

▪Les notes étalonnées se distribuent normalement (c'est donc une normalisation de la distribution par transformation non linéaire des notes brutes).