Nombre des composantes

Un des points les plus délicats de l'ACP ou encore l'analyse factorielle exploratoire est de fixer le nombre de composantes  à retenir dans l'analyse (on dit parfois le nombre des facteurs à extraire). Pour fixer ce nombre on doit apprécier la perte d'information induite par le fait que l'on réduit le nombre de dimensions. Par exemple si on a 15 variables, ne retenir que 4 facteurs supposent que le nuage de points dans cet espace à 4 dimensions n'est pas trop éloigné du nuage initial et que les variables sont suffisamment "expliquées" par les composantes. Il faudra prendre en compte (d'une façon ou d'une autre) :

®la qualité de représentation du nuage dans ce sous-espace factoriel (exprimé en pourcentage de variance expliqué) ;

®la qualité de la représentation qu'apporte chaque composante (valeur propre);

®la qualité de la représentation de chacune des variables (communauté).

Règles  pour définir le nombre des facteurs extraits

Soit la table des valeurs propres suivantes (indiquant pour chacun des 10 composantes, la valeur propre, le pourcentage de variance expliqué par le facteur (taux d'inertie) et le pourcentage cumulé de variance expliquée.

Il n'existe pas une seule méthode mais plusieurs qui ne sont pas toujours convergentes et qui ne sont pas toutes recommandées. Les méthodes les plus utilisées sont :

•le critère de Kayser (ou Kayser -Guttman)

Ce critère simple est souvent évoqué (et utilisé) est imparfait et ne devrait plus être utilisé. On ne retient que les facteurs dont la valeur propre est supérieure à 1. Dans l'exemple précédent on ne retient que les 4 premières composantes. Cette méthode n'est pas une méthode recommandée.

•Le test d'accumulation de variance ou scree-test (un autre nom est parfois donné "test du coude").

Le scree-test (test d'accumulation de variance de Cattell, 1966) consiste à regarder comment évoluent les valeurs propres en fonction de leur ordre d'extraction. Le terme « scree » fait référence à l'accumulation de dépôts rocheux au pied d'une montagne créant ainsi un petit promontoire à l'endroit où le dénivelé de la montagne se transforme en une pente plus douce.  On ne retient justement que les composantes qui précédent le passage à cette pente douce.

Dans la figure suivante, représentant l'évolution des valeurs propres pour les composantes  extraites (du premier au 10ème), le changement de pente s'effectue avec la 5ème composante, on devrait donc ne retenir que les 4 premières. Cette technique est souvent utilisée. Facile à mettre en œuvre elle devrait cependant être utilisée en complément d'autres techniques.

Remarque : le graphique des valeurs propres s'appelle aussi parfois en français "l'éboulis des valeurs propres".

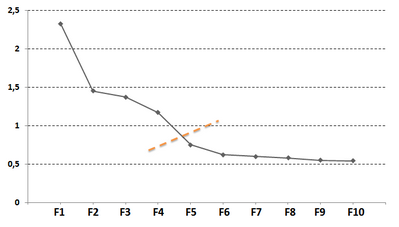
Figure H.1 : Scree test (évolution des valeurs propres pour les facteurs 1 à 10)

•L'analyse parallèle

Cette approche, en complément du test d'accumulation a été proposée par Horn (1965). Cette méthode s'appuie sur le fait que, même en partant de données générées au hasard, il est possible d'observer une composante pouvant expliquer une proportion de variance supérieure à 1.  L'analyse parallèle consiste donc à réaliser  une série importante (1000 ou plus) d'ACP sur une matrice de corrélations générée au hasard mais comportant le même nombre de variables et le même nombre de participants que l'étude principale.  La série des valeurs propres observée sur les données de l'étude est comparée à celle issue des valeurs propres calculées sur les données aléatoires (il existe plusieurs programmes, faciles à trouver sur le web, permettant de calculer ces valeurs). On ne conserve que les composantes dont la variance est significativement supérieure à celle obtenue avec la matrice de corrélations générée au hasard.  La figure suivante illustre ce processus de décision. On ne retient que les 4 premiers facteurs. Cette technique fait partie des techniques recommandées.

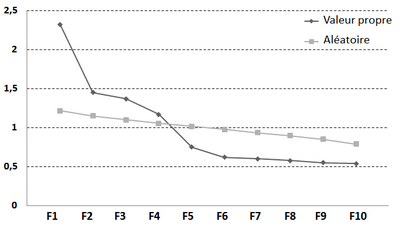
Figure H.2 : Évolution des valeurs propres et analyse parallèle

•la qualité de représentation du nuage de points

Très ambigu, ce critère consiste à retenir les facteurs de façon à expliquer au moins un certain pourcentage de variance. Selon la nature des mesures et de leur fidélité la valeur de ce critère peut varier. Ici, si on fixe le critère à 70% de variance expliquée, il faudrait retenir 5 composantes. Cette méthode peu être utilisée en complément des méthodes précédentes et considérée comme un  "regard" sur la qualité de la représentation retenus dans l'analyse. A elle seule, elle n'est pas recommandée pour déterminer le nombre de composantes à retenir.

•Autres critères pouvant être utilisés mais beaucoup moins courants (cf aussi Velicer, W., Eaton, C., & Fava, J., 2000)

®VSS (Very Simple Structure Critérion). Proposé par Revelle et Rocklin en 1979, le principe de cette méthode est de recalculer la matrice de corrélation initiale en ne gardant pour chaque variable, que la saturation la plus élevée (dans certaines variantes on garde les deux saturations les plus élevées), toutes les autres saturations étant fixées à 0. La valeur de VSS est un test d'ajustement de cette matrice recalculée à la matrice originale de corrélations  (prend des valeurs entre 0 et 1). Cette valeur est calculée pour des solutions allant de 1 composante  au nombre maximum de composantes. Elle tend vers une valeur optimale associée au nombre de facteurs à retenir. Peu utilisée, cette méthode convient peu pour des structures factorielles complexes.

®Comparative Data (CD) introduite par Ruscio et Roche (2012) est une extension de la méthode parallèle de Horn. Elle consiste à prendre en compte la structure factorielle dans la génération de données aléatoires.

®Minimum Averafe Partial (MAP). Introduite par Vélicer en 1976, cette méthode consiste à recalculer la matrice des corrélations en retirant les k premières composantes  (1, puis 2, etc.). Pour chaque valeur de k, on calcule moyenne des carrés des corrélations se trouvant en dehors de la diagonale. Cette moyenne va diminuer puis ré-augmenter. Le nombre de composantes à retenir correspond à la valeur la plus basse observée.

Contrôle de la pertinence du nombre des facteurs sélectionnés.

oLe nombre des composantes retenues doit permettre d'expliquer globalement un pourcentage de variance suffisant (varie selon les domaines mais si on n'explique que 30% de la variance on peut s'inquiéter de la représentativité des composantes)

oLa communauté correspond à la quantité de variance d'un test expliqué par les n premières composantes. Chaque communauté devrait avoir une valeur proche (plus ou moins) du pourcentage de variance cumulée expliqué par les composantes retenues (divisé par 100). Si une variable est clairement peu expliquée cela signifie soit que le nombre des composantes sélectionnées n'est pas suffisant, soit que cette variable corrèle peu avec les autres variables et devrait être exclue de l'analyse.

Pour ceux qui veulent aller plus loin

Ils existent de nombreux articles sur la façon de déterminer le nombre de facteurs. L'analyse parallèle de Horn est celle qui semble la plus appropriée (parmi les méthodes simples). Cependant, dans des simulations récentes, la méthode CD (comparative data) est préférable. Cette méthode est plus complexe à mettre en œuvre mais  Ruscio (auteur de la méthode avec Roche) a déposé un script sous R* permettant de déterminer ce nombre de facteurs (http://ruscio.pages.tcnj.edu/quantitative-methods-program-code/). Vous pouvez toujours, pour ceux qui connaissent R, en profiter pour voir comment on simule des données et la méthode utilisée.

(*) R est un système d'analyse statistiques et un langage dérive de S. Il est distribué librement sous les termes de la GNU General Public Licence et est disponible pour plusieurs environnements (Windows, Linux, MacIntosh).