Importance de la prévalence

L'utilisation des indicateurs de spécificité et sensibilité est une source d'erreur (biais cognitif). Le plus simple pour illustrer ce biais est de vous y confronter.

Soit  un test dont la sensibilité serait de 99% et sa spécificité serait aussi élevée(98%). 

Question : On vous fait passer le test. Vous n'étiez pas inquiet car la prévalence dans la population est  (1 pour 100).  Vous êtes malheureusement positif au test ! Quelle est la probabilité d'avoir le trouble (ou la maladie) ?

Réponse probable :  au regard des valeurs de spécificité et de sensibilité la majorité des personnes répondent (à tort)  que la probabilité d'avoir le trouble  est élevée. 

 En fait ce n'est pas si simple. Vérifions ce qu'il en est avec un simple calcul.

○On peut  constater que l'épreuve détecte correctement les vrais positifs dans 99% des cas (sensibilité) et les vrais négatifs dans 98% des cas (spécificité).

○Pour répondre à la question je peux utiliser le théorème de Bayes :

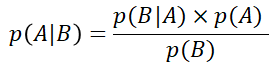
avec :  A = présence du trouble ; B =  test positif

▪nous savons que 

‣ P(B∣A) =  0.99 (c'est la sensibilité du test)

‣P(A) = 0.01 (prévalence) 

▪par ailleurs 

‣p(¬A) = 0.99  (proportion de personnes sans trouble  soit 1 - p(A))

‣P(B∣¬A) = 0.02 (correspond à 1 moins la spécificité soit 1 - Sp)

▪donc

‣p(B) = p(B∣A)*p(A) + P(B∣¬A) * p(¬A) = 0.99*0.01 + 0.02*0.99 = 0.297 

(ce qui correspond  à la probabilité d'être positif si on présente le trouble auquel s'ajoute la probabilité d'être positif si on ne présente pas le trouble). 

▪Ce qui permet de calculer p(A∣B)

‣P(A∣B) = 0.99*0.01/0.297

‣P(A∣B) = 0.33

Bonne Réponse :  la probabilité d'avoir le trouble  est de 33%. 

Être positif ou négatif ne permet pas d'estimer, connaissant uniquement la spécificité et la sensibilité, la probabilité que le trouble soit présent ou non. Spontanément vous auriez probablement répondu que la probabilité d'avoir le trouble si le test est positif est bien supérieure à 0.33 (33%). En fait, si la prévalence est faible, malgré une bonne spécificité et sensibilité, en cas de test positif, la probabilité d'avoir le trouble reste faible. Si la prévalence était de 2%, la probabilité d'avoir le trouble passerait à .50 (50%). A l'inverse si la prévalence est de 1‰, le calcul  donne la valeur de 4.17 (soit 4,17% de "chance" seulement d'avoir réellement le trouble si le test est positif !).

 La prise en compte de la prévalence de la maladie est donc essentielle pour interpréter la spécificité et la sensibilité des tests.