Scores Standards Normalisés

Lorsque la distribution ne respecte pas la condition de normalité mais ne s'éloigne pas trop de celle-ci, on peut normaliser la distribution assez simplement en calculant les scores standards normalisés. Cette procédure permet d'obtenir un score similaire au score z (à partir des effectifs cumulés). Ce score peut ensuite être transformé en score z, ou en toute autre étalonnage supposant une distribution normale.

Cette procédure pour obtenir un score z est facile à mettre en œuvre  :

oÉtape 1 : établir les effectifs et les effectifs cumulés

oÉtape 2 : calculer les fréquences cumulées (on peut aussi utiliser les rangs percentiles)

oÉtape 3 : pour chaque score, lire dans une table de la loi normale la valeur z correspondant au rang percentile ou aux fréquences cumulées. Il est aussi possible d'utiliser les fonctions pré-programmées des tableurs ou des fonctions spécifiques avec le logiciel R (R Core Team, 2025).

Avec cette procédure,  pour chaque score possible, un score standard normalisé est calculé (c'est une une note z). Ce score peut être utilisé pour calculer des scores T comme dans l'exemple suivant.        

Exemple (réalisé avec un tableur). La première colonne correspond aux scores observés, la seconde aux effectifs, la troisième colonne est l'effectif cumulé et enfin la quatrième colonne est le pourcentage cumulé. Les deux dernières colonnes sont respectivement la note standard normalisée (ou score z obtenu en utilisant la fonction d'un tableur (LOI.NORMALE.INVERSE.N) puis le score T en multipliant la note standardisée par 10 puis en ajoutant 50. 

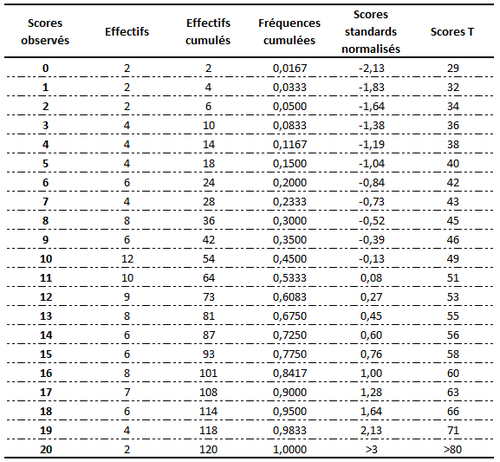
Si vous n'avez pas de tableur, pour trouver le score standard normalisé d'une note (par exemple la note 17 dans l'exemple précédent), on cherche dans une table de la loi normale, la valeur z correspondant au pourcentage cumulé (ici 0.900).  C'est bien entendu  la même que celle calculée avec un tableur !

Pour aller plus loin

La présentation faite ici est une présentation classique simple. En fait, il existe plusieurs procédures pour passer du score observé aux scores standards normalisés, les formules de transformation variant sur un simple paramètre. Il s'agit du paramètre c dans la formule ci-dessous (Procédure de Van der Waerden, c=0 ; Blom, c=3/8 ; Tukey, c= 1/3 ;  ou enfin procédure Rankit avec c = 1/2).

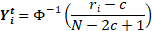
Il peut y avoir aussi des notes non observées dans l'échantillon. Aux extrémité ce n'est pas grave mais entre les bornes minimum et maximum observées, il faut alors fixer des règles de calcul pouvant être légèrement différentes. On peut aussi s'interroger sur la taille de l'échantillon (il est possible qu'il soit insuffisant pour que toutes les notes soient observés). Ce n'est pas le cas dans notre exemple.

Pour en savoir plus, si cela vous intéresse, cf. l'article de Solomon & Savilowsky  de 2009.